La correlación Ta - Rmax
El ciclo de actividad puede ser caracterizado por varios parámetros: su duración, el tiempo de subida, el de bajada, los números de Wolf máximo y mínimo, el área bajo toda la curva y bajo las ramas ascendente y descendente, su asimetría, etc... Una vez calculados, se pueden emparejar dos a dos para intentar hallar correlaciones entre ellos. Este proceso desemboca en las que se conocen como "Leyes de Waldmeier"; una serie de reglas empíricas establecidas por Waldmeier en 1935, que pueden enunciarse como sigue:
-
Cuanto mas activo sea el ciclo, más corto es el tiempo de subida.
-
Cuanto mas activo sea el ciclo, más largo es el tiempo de bajada.
-
Cuanto mas activo sea el ciclo, mayor es la actividad 5 años después del máximo.
-
Cuanto mas activo sea el ciclo, mayor es el área bajo la rama descendente.
-
El área bajo la rama ascendente es casi independiente de la altura del máximo.
|
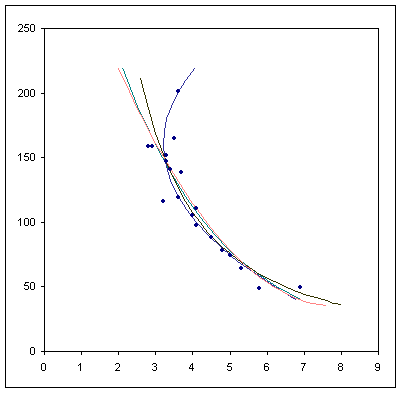
No obstante, al representar los datos se aprecia una dispersión bastante alta con la única excepción de la 1ª y la 4ª ley. En particular, la 1ª, que establece una correlación entre el tiempo de subida (Ta) y el número de Wolf máximo (Rmax), es lo bastante significativa para poder modelizar una serie de curvas que constituyen, hoy por hoy, el método más preciso para pronosticar con cierta antelación el máximo de un ciclo. Esta es la razón para intentar ajustar de la manera más precisa posible la nube de puntos.
| Ciclo Nº |
Ta |
Rmax |
| 1 |
6,3 |
86,5 |
| 2 |
3,2 |
115,8 |
| 3 |
2,9 |
158,5 |
| 4 |
3,4 |
141,2 |
| 5 |
6,9 |
49,2 |
| 6 |
5,8 |
48,7 |
| 7 |
6,6 |
71,7 |
| 8 |
3,3 |
146,9 |
| 9 |
4,6 |
131,6 |
| 10 |
4,1 |
97,9 |
| 11 |
3,4 |
140,5 |
| 12 |
5,0 |
74,6 |
| 13 |
4,5 |
87,9 |
| 14 |
5,3 |
64,2 |
| 15 |
4,0 |
105,2 |
| 16 |
4,8 |
78,1 |
| 17 |
3,6 |
119,2 |
| 18 |
3,3 |
151,8 |
| 19 |
3,6 |
201,3 |
| 20 |
4,1 |
110,6 |
| 21 |
3,5 |
164,5 |
| 22 |
2,8 |
158,5 |
| 23 |
3,7 |
138,5 |
|
|
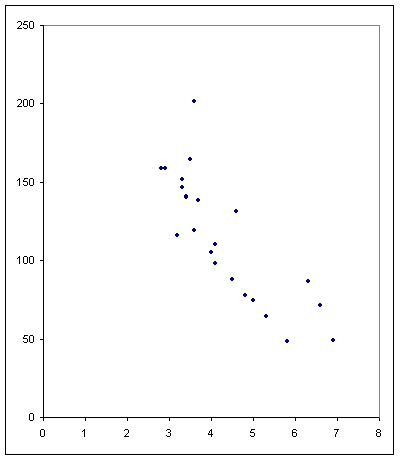 |
Al observar la gráfica, destacan 5 ciclos que parecen apartarse significativamente de los demás: los nº 1, 5, 7, 9 y 19. El caso del ciclo 19 lo trataremos más adelante, y el del nº 5, que también parece discrepante, en realidad no lo es tanto, como luego veremos en el ajuste. Los ciclos 1, 7 y 9 son más difíciles de interpretar y eso llevó a Waldmeier a realizar dos ajustes, uno para ciclos pares y otro para impares, aunque posteriormente, la inclusión de nuevos ciclos le indujo a unificarlos.
La explicación a esos tres ciclos, en mi opinión, se encuentra en que son anteriores a 1848 (el nº 9 alcanzó el máximo en ese año y, por tanto, su rama ascendente es anterior). 1848 es el año en que se empezó a utilizar el número de Wolf. Esto significa que los ciclos anteriores tuvieron que reconstruirse " a posteriori " a partir de observaciones heterogéneas, y deben ser tomados con todas las reservas. De hecho, los ciclos 1, 5 y 7 son los únicos en los que el máximo (deducido a posteriori) tuvo lugar después de la mitad del ciclo. En todos los demás, el tiempo de subida siempre ha sido más corto que el de bajada.
En el resto del artículo mantendré el nº 19 porque al ser un ciclo reciente es bastante más "fiable", pero prescindiré de los ciclos nº 1, 7 y 9. Esto no modificará las conclusiones, únicamente afectará a los valores de las constantes y coeficientes de correlación, así como al mejor o peor ajuste del ciclo 19.
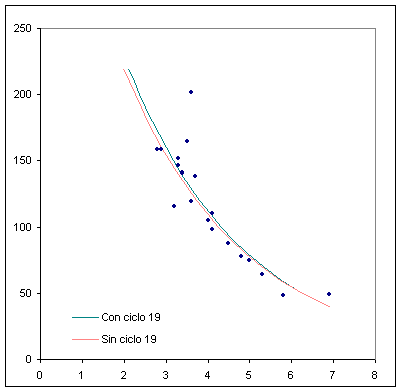
Waldmeier ajustó la nube de puntos mediante una función logarítmica. Utilizando el mismo tipo de función para ajustar todos los ciclos habidos hasta ahora (excepto 1, 7 y 9) se obtiene el siguiente resultado:
log Rmax = 2,67 (± 0,06) - 0,15 (± 0,02) ·Ta r = 0.855 (con ciclo 19)
log Rmax = 2,64 (± 0,05) - 0,15 (± 0,01) ·Ta r = 0.912 (sin ciclo 19) |
En la gráfica vemos como la mayoría de los ciclos que quedan a la derecha están por debajo de la curva, al contrario que los que quedan a la izquierda. Por otra parte, el ciclo nº 19 aparece como un ciclo anómalo, tanto si se incluye como si no en el ajuste.
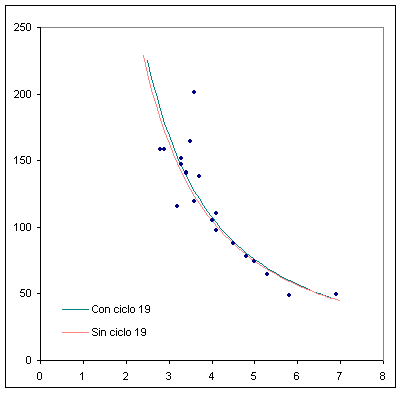
Otro tipo de función que se puede emplear es una que sea doblemente logarítmica, aunque no mejora apreciablemente el resultado:
| log Rmax = 2,98 (± 0,09) - 1,57 (± 0,16) ·log Ta r = 0.850 (con ciclo 19)
log Rmax = 2,94 (± 0,07) - 1,53 (± 0,12) ·log Ta r = 0.912 (sin ciclo 19) |
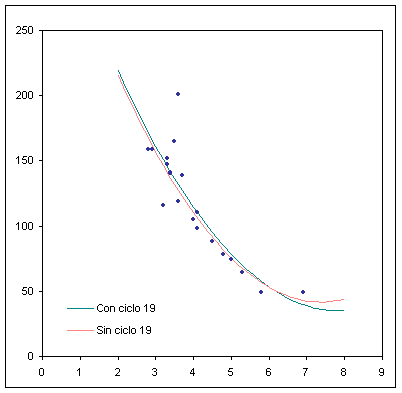
Xanthakis, en 1967, consiguió también un buen coeficiente de correlación utilizando los ciclos 7 -19 y una función parabólica. Aplicando esa función a los ciclos que estamos considerando se obtiene:
| Rmax = 35 (± 12) + 5.4 (± 0,7) ·(Ta - 7.84) 2 r = 0.761 (con ciclo 19)
Rmax = 42 (± 7) + 6.0 (± 0,5) ·( Ta - 7.37) 2 r = 0.891 (sin ciclo 19) |
En todos estos ajustes persiste el problema del ciclo nº 19, y además, el nº 5 parece condicionar el ajuste en la parte baja de la gráfica. Por otra parte, las funciones elegidas son estrictamente decrecientes en la región considerada, y esto significa que para Rmax del orden de 250 o superiores, nos encontraríamos con periodos de subida inferiores a dos años, lo cual es un poco difícil de creer. Estas razones me han llevado a probar otro tipo de función: una parábola horizontal (la inversa de la que utilizó Xanthakis).
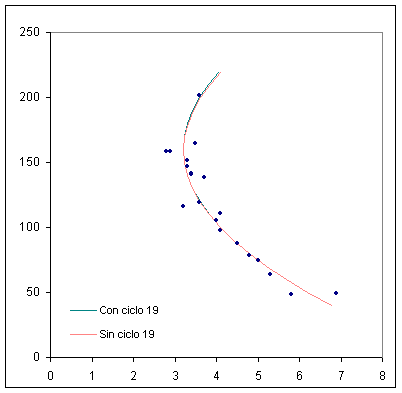
Los coeficientes "a" y "b" los he obtenido por mínimos cuadrados y "R*" lo he calculado numéricamente por el método de Newton optimizando el coeficiente de correlación. El resultado es el siguiente:
| Ta = 3.20 (±0.09) + 0.00025 (±0.00002) ·(Rmax - 160.36) 2 r = 0.926 (con ciclo 19)
Ta = 3.21 (±0.09) + 0.00025 (±0.00002) ·(Rmax - 159.38) 2 r = 0.925 (sin ciclo 19) |
Con esta función, el coeficiente de correlación es el mayor conseguido hasta ahora y reproduce muy bien la mayoría de los ciclos observados. Además, tanto si incluimos el ciclo 19 como si no, la función es prácticamente la misma, y esto significa que dicho ciclo deja de ser anómalo y se incorpora de manera totalmente natural al ajuste.
Una función de este tipo tiene dos consecuencias principales. La primera es que existe un periodo de subida mínimo en torno a los 3.2 años. Los ciclos nº 3 y 22, con 2.9 y 2.8 años respectivamente estarían situados en el límite inferior. La segunda es que aparecen dos tipos de ciclos separados por un valor de Rmax de unas 160 unidades. Para un periodo de subida determinado podríamos tener tanto un ciclo alto como un ciclo bajo.
En la gráfica inferior he superpuesto las cuatro funciones para poder compararlas mejor. Por debajo de R = 160, la diferencia entre todas ellas es menor que la dispersión de los datos y, por eso, es bastante difícil elegir entre una u otra. Para saber cual responde mejor a la realidad, tenemos que irnos por encima de las 160 unidades. El problema es que en esa región solo tenemos un único ciclo que, después de todo, podría ser poco representativo. Sabemos que en otras épocas, como en la Edad Media, el Sol tenía bastante más actividad que ahora. Habrá que tener paciencia y esperar que nuestra estrella nos ofrezca uno o varios ciclos muy activos para poder juzgar mejor los diferentes ajustes.
Una vez obtenida una función de ajuste, es posible deducir una expresión que nos permita realizar pronósticos sobre la altura de siguiente máximo a partir del aumento en el nº de Wolf durante la rama ascendente. Usando la parábola horizontal:
|
v = dR/dt = (Rmáx - Rmín) / (38.4 + 0.003 · (Rmáx - 160.3)2) |
v es el aumento del nº de Wolf con el tiempo en un momento determinado de la subida al máximo. Para obtenerlo se divide el nº de Wolf medio correspondiente a ese mes (hay que usar los valores suavizados) entre los meses transcurridos desde el mínimo. En la anterior expresión se puede despejar Rmax en función de v, pero el resultado es algo complicado e incómodo de manejar. Es preferible utilizar una tabla como la siguiente:
| v |
R |
| 0,6672 |
50 |
| 0,7671 |
55 |
| 0,8744 |
60 |
| 0,9896 |
65 |
| 1,1130 |
70 |
| 1,2446 |
75 |
| 1,3847 |
80 |
| 1,5333 |
85 |
| 1,6901 |
90 |
| 1,8549 |
95 |
| 2,0272 |
100 |
| 2,2062 |
105 |
| 2,3909 |
110 |
| 2,5801 |
115 |
| 2,7722 |
120 |
| 2,9655 |
125 |
| 3,1580 |
130 |
| 3,3474 |
135 |
| 3,5315 |
140 |
| 3,7077 |
145 |
| 3,8738 |
150 |
| 4,0274 |
155 |
| 4,1666 |
160 |
| 4,2897 |
165 |
| 4,3952 |
170 |
| 4,4822 |
175 |
| 4,5504 |
180 |
| 4,5995 |
185 |
| 4,6301 |
190 |
| 4,6429 |
195 |
| 4,6389 |
200 |
| 4,6194 |
205 |
| 4,5859 |
210 |
Javier Ruiz