INTRODUCCIÓN

En el momento de escribir estas líneas aún está reciente en mi retina el pasado eclipse anular, magnífico espectáculo que me trae a la memoria aquel otro que pudimos disfrutar hace ya año y medio: el tránsito de Venus. Ahora en el olvido, este artículo pretende recordar y dar a conocer la importancia histórica del fenómeno así como los resultados obtenidos en la campaña de observación “venus transit 2004”

UN POCO DE HISTORIA…

A finales del siglo XVI la visión mayoritaria que se tenía del Sistema Solar era la concepción geocéntrica de Ptolomeo. La Tierra, inmóvil, ocupaba el centro en torno al cual giraban el resto de astros anclados en esferas concéntricas perfectas. Los planetas seguían farragosas órbitas, compuestas por numerosos círculos superpuestos (epiciclos y deferentes) hasta lograr cuadrar las observaciones. Un cielo mítico y lleno de una “perfecta abstracción”.

Con las primeras observaciones telescópicas de Galileo y las leyes de Newton y Kepler, las ideas copernicanas toman fuerza y se alcanza la comprensión que, más o menos, tenemos hoy en día. La Tierra ya no es el centro y ahora se mueve, como el resto de los planetas, en una sencilla órbita elíptica en torno al Sol, atraída por la masa de éste.

LA TERCERA LEY DE KEPLER

En 1619, basándose en las observaciones de Tycho Brahe, Kepler publica su     tercera ley del movimiento planetario sentando la escala del Sistema Solar:

“Los cuadrados de los tiempos empleados por los planetas en recorrer sus órbitas son directamente proporcionales a  los cubos de sus distancias medias al Sol”

que matemáticamente expresamos:

tomando como referencia los valores conocidos para la Tierra (que por definición valen la unidad), podemos escribir:

Así, a partir del periodo observado para un planeta podemos calcular la distancia a la que se encuentra. Nos queda por fin un Sistema Solar concreto, bien definido. Ahora podemos ordenar los planetas en función de su distancia al Sol, de forma precisa:

Tabla 1: Distancias planetarias

todo en función de la Unidad Astronómica (UA): la distancia media de la Tierra al Sol, el factor de escala del Sistema Solar.

El siguiente paso es inmediato: calcular el valor absoluto de esta unidad. ¿Cuántos Kms es una UA? Esto era muy importante, no sólo para establecer las distancias planetarias sino también para poder hallar las masas, densidades, fuerzas…la dinámica del Sistema Solar, todo ello en función de valores absolutos de la distancia.

Este problema no es nuevo y ya desde la antigüedad, los griegos intentaron hallar, sin mucho éxito, la distancia al Sol (y a la Luna), pero ni siquiera conocíamos con certeza el tamaño de nuestro planeta. Por eso se daban los resultados obtenidos en radios terrestres, como se puede ver en la siguiente tabla. Solían aprovecharse la “cuadratura” Sol-Tierra-Luna para efectuar sencillos cálculos trigonométricos.

Para tener una idea del acierto o no de estos intentos, una UA son 23400 radios terrestres:

Tabla 2: Valores antiguos de la UA

A continuación veremos qué papel va a jugar Venus (y en concreto, sus tránsitos por delante del Sol) en este empeño por alcanzar el valor absoluto de la escala del Sistema Solar.

LOS TRÁNSITOS DE VENUS

El 7 de noviembre de 1677 Halley, entre nubes, observó un tránsito de Mercurio dándose cuenta que podría servir para determinar el valor de la UA. Midió el recorrido del planeta sobre el disco solar (31'14''5) y lo restó del que daban las efemérides para el tránsito visto desde el centro de la Tierra (30'50'') hallando la diferencia  de las paralajes del Sol y de Mercurio: 24''5. Determinó con precisión el tiempo empleado por el planeta en atravesar el Sol, 5h 14m 20s y con algo de geometría euclidea y la tercera ley de Kepler halló una paralaje solar, π = 45” (un quinto del valor real).

Se da cuenta que este valor no es muy correcto y llega a la conclusión de que Mercurio está muy cerca del Sol y la diferencia de paralajes no es muy grande. Sería mejor usar Venus, ya que tiene un desplazamiento paraláctico mayor con un movimiento más lento sobre el disco. A partir de los tiempos de “entrada” y “salida” de Venus (I y IV contacto respectivamente) un observador podrá determinar la duración del tránsito con un segundo de precisión y su longitud exacta. Si esto lo hacen, al menos, dos observadores situados en localidades más o menos distantes podrán hallar π con una precisión de una parte sobre 500, comparando la separación de las cuerdas observadas de Venus sobre el Sol. Estas conclusiones bien desarrolladas las publica en 1716 en su libro “Un nuevo método para determinar la paralaje del Sol” (cuyo texto podemos encontrar en la siguiente web:

http://sunearth.gsfc.nasa.gov/eclipse/transit/HalleyParallax.html

Habría que esperar a los próximos tránsitos, los de 1761/1769 para ver los resultados pero Halley estaba muy seguro de su método y pensaba que daría mejores resultados que los habituales  basados en la paralaje de Marte ya que éste último necesitaba medir valores angulares, afectados de un mayor error instrumental, mientras que en su método se tomaban medidas de tiempos, más precisas.

En 1723 el francés Delisle propone otro método usando también el tránsito de Venus: bastaría con saber el tiempo del II ó III contacto (en vez de la duración completa del tránsito) desde dos puntos distintos cuya diferencia de longitud se conoce con exactitud, cosa todavía complicada en pleno siglo XVIII.

Los tránsitos de 1761/1769 decepcionaron ampliamente las expectativas. Al igual que en los tránsitos posteriores los principales países europeos organizaron expediciones para seguir el fenómeno (véase el número de mayo del 04 de esta misma revista, pág 36, para ver las expediciones españolas). Los valores obtenidos variaban entre 8”3 y 10”2, un intervalo demasiado amplio para dar una definición aceptable de la paralaje. Una pequeña variación de segundos de arco cambiaba mucho el valor de la UA. A esta incertidumbre contribuyó el efecto de la famosa gota negra, que dificultaba enormemente cronometrar el momento exacto del contacto, al no tener un borde bien definido. También faltaba un aparato matemático capaz de tratar muchos datos en plan estadístico: todavía faltaban varios años para que Gauss publicara su teoría de los mínimos cuadrados.

Los siguientes tránsitos ocurrieron en 1874/1882. La aplicación de modernas técnicas fotográficas y de espectroscopia visual  junto con el desencanto de los tránsitos anteriores, levantaron grandes expectativas. Sin embargo, el resultado, a pesar de acotarse, no llegó a convencer: 8”86-9”05. Se llegó a la conclusión de que los tránsitos de Venus no eran la mejor manera para calcular la paralaje y que había que seguir buscando nuevos métodos.

En la tabla 3 aparecen nombrados los distintos métodos aparecidos a partir del siglo XVI, además de los tránsitos ya comentados, y en la tabla 4 los principales resultados, que poco a poco se van acercando al correcto. Según se consulten bibliografías distintas estos valores cambian un poco pero sirven igualmente para darnos una buena idea de cómo ha ido evolucionando nuestra distancia al Sola lo largo del tiempo. Cabe destacar el desarrollado a partir de los desplazamientos sobre el fondo estelar de asteroides, con buenos resultados por parte de J. G. Galle y D.Gill.  

Tabla 3: Métodos desarrollados para el cálculo de la UA

Hoy en día obtenemos valores de la UA considerada ya como unidad secundaria y lo que medimos es el tiempo luz al Sol, mediante rádares, viendo lo que tarda en volver un haz enviado. A partir del valor de la velocidad de la luz, sabemos la distancia exacta a la que se encuentra nuestra estrella.

En plena era digital resulta paradójico que volvamos sobre nuestros pasos y recalculemos la UA con métodos sencillos comparándolo, como se verá después de forma más que satisfactoria, con la última tecnología rádar.

Tabla 4: Valores modernos de la UA

CÁLCULO SIMPLIFICADO DE LA PARALAJE

De un modo simplificado y esquemático se puede comprender fácilmente el fundamento en el que se basa  el cálculo de la UA a través de un tránsito de Venus.

Tenemos situados dos observadores situados en localidades más o menos lejanas. La línea que los une, b, de longitud conocida obviamente, será la base de la triangulación. El observador A ve proyectado Venus sobre el disco solar en A' y de manera análoga B en B'.

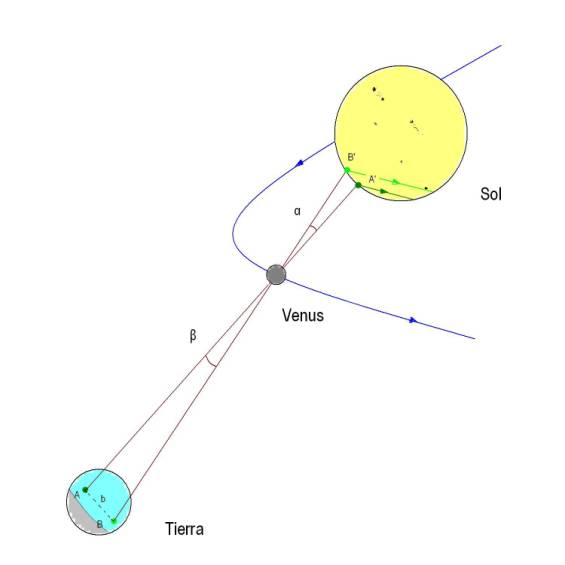
Figura 1 :Esquema del momento del tránsito

Comparando las dos observaciones vemos que Venus ha recorrido dos caminos distintos (aunque no tan exagerado como en el dibujo) empleando para ellos diferentes tiempos. A partir de esta diferencia de tiempos podemos calcular la distancia angular entre A' y B' y con ella el valor del ángulo α, que es igual a β. A su vez, este valor es la medida angular de la base formada por los observadores A y B vista desde el centro de Venus. Puesto que el tamaño angular es proporcional al tamaño del objeto e  inversamente proporcional a la distancia desde donde se observe, podemos expresarlo de la siguiente manera,

donde dTV es la distancia Tierra-Venus en el momento del tránsito, que al estar alineados en el mismo plano, será igual a la resta de la distancia al Sol de la Tierra, y de la de Venus. Estas distancias las conocemos por la 3ª ley de Kepler (tabla 1): 1-0,723 = 0,277 UA.

De forma análoga, sabemos que la paralaje solar, π, la podemos escribir como:

siendo r, el radio terrestre, la base de la triangulación ahora, y dTS la distancia de la Tierra al Sol, en nuestro caso 1 UA.

Dividiendo ambas expresiones nos queda:

que será la expresión que nos dará el valor buscado de la paralaje a partir del cual hallaríamos el valor de la UA.

Básicamente este el método utilizado. La forma en que hallamos β es lo que va a diferenciar un poco más los distintos métodos.

LA RED VT-2004

Debido al poder mediático y a la gran expectación generada por el tránsito surge para divulgar el fenómeno y organizar una red a nivel mundial para recalcular el valor de la UA de manera similar a como se ha explicado en el apartado anterior.

Ha sido respaldada por la Comisión Europea en el marco de la semana europea de la ciencia 2004 así como por diversos organismos europeos como el Observatorio Europeo Austral (ESO), la Asociación Europea para la Enseñanza de la Astronomía (EAAE), el Instituto de Mecánica Celeste y de Cálculo de Efemérides francés (IMMCE), el Observatorio de París y el Instituto Astronómico de la Academia de las Ciencias de la República Checa.

La red contaba con una web, http://www.vt-2004.org/ donde la gente podía informarse sobre todo lo concerniente al tránsito así como registrarse para posteriormente colaborar con el envío de cronometrajes, fotos, vídeos o cualquier otro dato relativo al fenómeno.

Finalmente ha habido 2763 colaboraciones en todo el mundo de las cuales 2427 han sido europeas, ya sea desde colegios-institutos, agrupaciones astronómicas o a título individual como se puede ver detallado en las figuras 3 y 4,

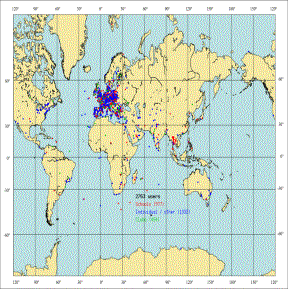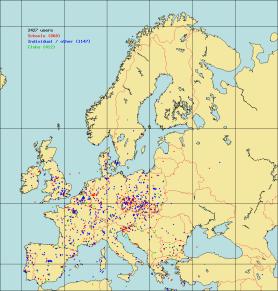Figura 3:   Participación mundial en la red                           Figura 4: Detalle de la participación europea

En total se han conseguido 4550 cronometrajes procedentes de 1510 observadores de los cuales se han estimado como suficientemente buenos para los cálculos, realizados por el IMMCE,  4367 tiempos de 1440 observadores, como se puede ver una base de datos suficientemente amplia.

PARTICIPACIÓN ESPAÑOLA

En España el Planetario de Pamplona fue el encargado de hacer de nodo canalizando toda la campaña. Entre otras observaciones cabe destacar:

• Observatorio de Calar Alto
• Planetario de Madrid
• Sociedad Malagueña de Astronomía - Málaga
• Asociación de Astrónomos Aficionados ASAAF-UCM
• Observatorio Astronómico Hotel Meliá Tamarindos - San Agustín -  Gran Canaria
• Departamento de Astronomía y meteorología de la  Universitat de Barcelona
• Agrupació Astronòmica de Sabadell
• Grupo Astronomico Silos de Zaragoza
• IES Coloma - Jerez de la Frontera
• Parque de las Ciencias - Granada
• Instituto de Astrofísica de Andalucía
• Astroalgaida- Puerto Real, Cádiz

RESULTADOS

A partir de todos los datos recibidos se siguieron varios métodos de cálculo. Me limitaré a explicarlos muy por encima y sin entrar en detalle, y a continuación se comparan todos en una tabla. Aquellos que estén más interesados, en http://www.vt-2004.org/auresults/au-3a.pdf  y  http://www.vt-2004.org/auresults/au-3b.pdf tienen una explicación más detallada, así como en la página web del IMCCE, que es quien finalmente ha hecho todos los cálculos. 

Métodos:

• Cálculo en tiempo real de los datos recibidos “on line” el mismo día del tránsito:  Según iban llegando los tiempos de cada contacto, se calculaba la UA y se iban promediando obteniendo así el valor definitivo. Aquellos datos que diferían “mucho” de las efemérides no se tomaban como buenos para evitar un mal resultado.

• Método iterativo, a posteriori, una vez conocidos todos los datos.  A partir de un valor inicial de la UA, se calculaban unos tiempos teóricos, que se comparaban con los obtenidos. Todos aquellos que estaban dentro de un límite (el valor bueno se fijó en ±4 segundos) servían para calcular un nuevo valor de la UA, que a su vez recalculaba predicciones de los contactos que se usaban para volver a calcular una mejor UA y así sucesivamente. El método se probó usando como dato inicial el valor real de la UA demostrándose su correcta convergencia.

• Método de Deslisle:  A través de la comparación de datos dos a dos como se explicó anteriormente y su posterior iteración como en el caso anterior.

• Método de Halley:  Se necesitaba observar el primer y el cuarto contacto, lo que reduce el número de datos. Además, al ser la mayoría de los datos europeos, la base de la triangulación es demasiada pequeña. Sólo cumplían las condiciones 10 observaciones y ninguna de ellas era muy fiable por lo que no se llegó a usar este método.

Tabla 5 A: Resultados de la red vt 2004

De igual manera, tomando el valor ya conocido de la UA se ha calculado los radios del Sol y de Venus obteniendo los siguientes valores:

Finalmente el valor definitivo de la campaña es:

10838 km mayor que el valor real ( valor de la UAI, tabla 4 ). El resultado obtenido ha sido el más exacto hasta ahora (error del 0,007%) a pesar de la relativa falta de experiencia de muchos de los observadores. Se debe, como es lógico,   a la mayor precisión en los cronometrajes y en el conocimiento de nuestra posición geográfica así como en la mejor óptica de nuestros equipos y en el empleo de técnicas digitales de registro y procesado de las imágenes.

Creo que es una buena demostración de la utilidad del trabajo de los aficionados, debidamente coordinados, así como una muestra de la calidad de los participantes, tanto a nivel de campo, tomando cuidadosamente los cronometrajes, imágenes… como a nivel informático tratando posteriormente los resultados. Nos debería animar a todos a seguir a pie de ocular J

BIBLIOGRAFÍA

• Como se ha mencionado a lo largo del texto, la web de la campaña:    http://www.vt-2004.org/
• La web del IMCCE donde se explican los cálculos:    http://vt2004.imcce.fr/vt2004i
• El número de marzo del 2004 de la revista  COELUM