El primer catálogo detallado sobre las propiedades más básicas de las manchas (posiciones y áreas) fue el del Obsrvatorio de Greenwich, que abarca más de un siglo, desde 1874 hasta 1976 Al finalizar su labor en este campo, la UAI encargó al Observatorio de Debrecen la continuidad del programa. Hoy es la referencia indiscutible a la hora de consultar posiciones de manchas. Las medidas se realizan sobre imágenes en luz blanca obtenidas en Debrecen, y para completar los días no cubiertos por Debrecen, se echa mano de imágenes de otros observatorios Se puede acceder a los datos en el siguiente enlace: http://fenyi.solarobs.csfk.mta.hu/DPD/index.html
A la hora de comparar nuestra serie de datos con la de Debrecen es necesario considerar una dificultad. Como las medidas se han hecho en horas diferentes, el movimiento propio de las manchas puede generar un cierto grado de dispersión. Para evitar este problema se ha utilizado el conjunto de manchas con escaso movimiento propio que figura en el siguiente listado: http://www.parhelio.com/mp0.txt Por otra parte, de las medidas de Parhelio se han excluido aquellas debidas a un único observador, dejando las que resultan de promediar al menos dos observadores. En total son 450 posiciones.
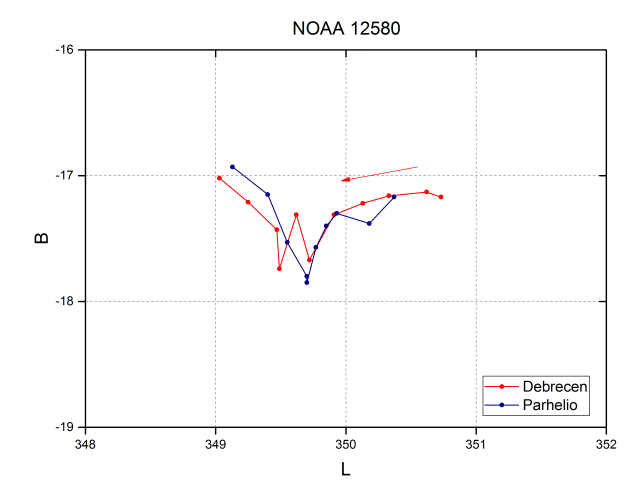
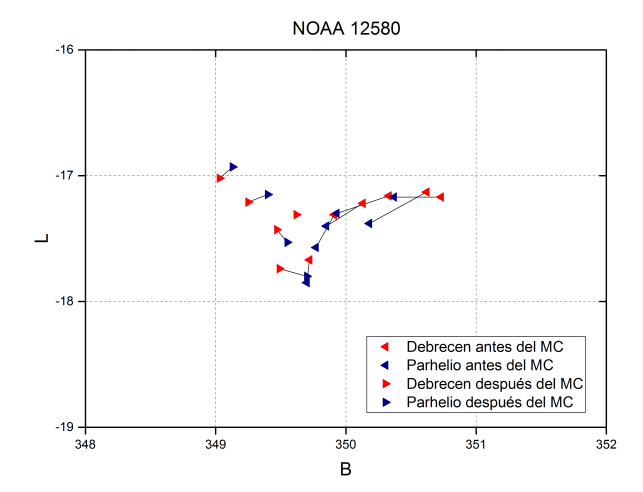
Al representar las posiciones de manchas individuales lo primero que se comprueba es una buena correspondencia. Sirva como ejemplo la gráfica de NOAA 12580 donde la flecha señala el sentido de movimiento. Cabe señalar que tanto en los datos de Debrecen como en los nuestros, se observa ocasionalmente una cierta dispersión en forma de saltos bruscos en la trayectoria (en la gráfica se pueden ver en las posiciones centrales). En nuestro caso medimos el centro fotométrico, pero no nos consta si lo que se mide en Debrecen es el centro geométrico o fotométrico de la umbra. Una variación en la forma o en la distribución de intensidades de la umbra, así como el seeing, son factores que pueden contribuir a esos saltos. No se ha cuantificado dicha dispersión, pero el examen de las gráficas sugiere que la magnitud es similar en ambas series, por lo que la influencia de los factores citados también es parecida.

Para comparar las dos series se ha calculado la distancia D en grados entre las posiciones de Parhelio y Debrecen en función de la distancia al centro del disco expresada como fracción del radio del disco. (Lp, Bp) son las coordenadas medidas por Parhelio y (Ld, Bd), las medidas por Debrecen. En estas diferencias existe una contribución debida a la dispersión ya mencionada, que afecta a ambas series, por lo que en realidad, el error producido por el propio método de medida sería inferior al calculado.
![]()
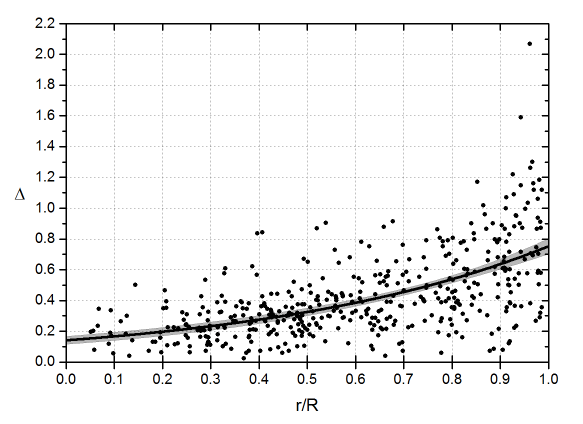
En la gráfica puede verse el resultado. Se ha añadido un ajuste con una función exponencial, y las correspondientes bandas de confianza para una probabilidad del 95%.
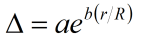
En la función, (a) es la ordenada en el origen, es decir, la diferencia en el centro del disco, y (b) indica el ritmo al que crece dicha diferencia a medida que nos acercamos al limbo. Los valores de los parámetros son:
a = 0.14º ± 0.01º
b = 1.67º ± 0.11º
Por una cuestión probabilistica (las manchas tardan poco en atravesar esa zona), en el centro del disco hay pocas medidas y el ajuste es menos fiable, pero las diferencias con Debrecen se mantienen por debajo de 0.3º hasta casi la mitad del radio, es decir, un ángulo heliocéntrico de 30º; y por debajo de 0.5º hasta un ángulo heliocéntrico de unos 50º (r/R = 0.77).
La magnitud D es la distancia en linea recta entre dos posiciones, pero si calculamos la distancia en longitud y latitud por separado y la representamos en función de la distancia al meridiano central, aparece un comportamiento curioso. En principio, cabria esperar que los datos formasen una nube de puntos en forma de banda horizontal y centrada en Y=0, es decir, que las diferencias no dependiesen de la posición de la mancha en el disco, salvo por la mayor dispersión que produce su proximidad al limbo. Sin embargo, vemos que no es así.
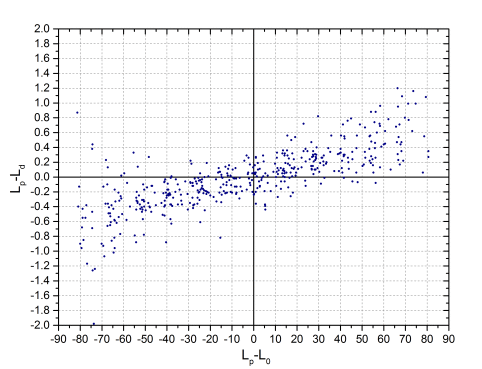
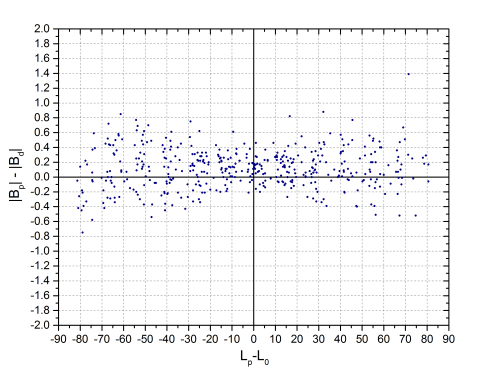
En la primera gráfica, se puede ver que cuando la mancha está al este del meridiano, nuestras longitudes tienden a ser menores que las de Debrecen, es decir, quedan más al Este. Por el contrario, al oeste del meridiano, nuestras posiciones quedan al oeste de las de Debrecen. En la gráfica de la derecha, para evitar que visualmente se compensen las diferencias de manchas situadas en hemisferios diferentes, no hemos tenido en cuenta el signo, es decir, se ha considerado que todas las latitudes son positivas. Ahí aparece la banda horizontal, pero no está centrada en el origen sino desplazada aproximadamente 0.1º del mismo. La interpretación cuantitativa de esta gráfica es complicada porque habría que tener en cuenta la latitud del centro del disco (B0), pero básicamente nos viene a decir que, en promedio, nuestras latitudes son ligeramente mayores que las de Debrecen
Ambos efectos pueden verse en la mancha NOAA 12580. Las líneas unen las posiciones correspondientes a los mismos días, y la orientación de los triángulos indica la situación de la mancha respecto al meridiano.
La solución a este pequeño enigma se obtiene al considerar ambas gráficas conjuntamente. Lo que nos están diciendo es que nuestras posiciones situan a las manchas más cerca del limbo que en el caso de Debrecen........ o el limbo más cerca de las manchas. En definitiva, los radios del disco que hemos utilizado son ligeramente menores que los de Debrecen.
Influencia del radio en las posiciones
Al calcular posiciones, en principio se puede utilizar el radio de dos maneras: se puede emplear el valor calculado a partir de las efemérides y de las características instrumentales, o bien obtenerlo directamente a partir de las imágenes. Como se explica en el artículo previo (http://www.parhelio.com/articulos/articresol.html), el primer método no es recomendable dada la incertidumbre con la que conocemos la focal y el tamaño de los píxeles.
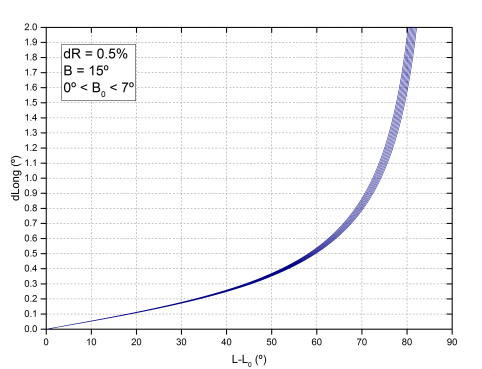
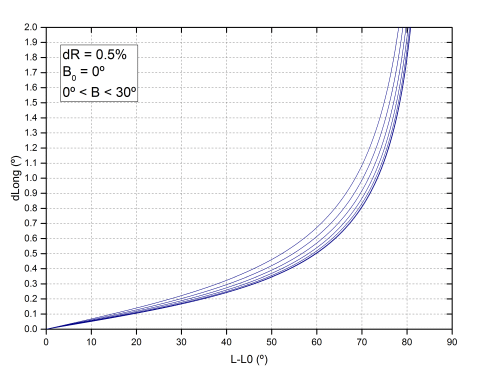
Para ver si se puede deducir, aunque sea aproximadamente, qué diferencia de radio tenemos con Debrecen, hay que comprobar como varían las coordenadas, si reducimos un porcentaje del radio. En el caso de la latitud, ésta siempre aumenta, que es lo que comprobamos anteriormente. La forma en que una variación del radio se transmite a la longitud se determina mediante una serie de expresiones que dependen también de la latitud de la mancha (B), y la latitud del centro del disco (B0). La dependencia con B0 y B es pequeña. En las gráficas siguientes se representa lo que varía la longitud (dLong) a medida que nos alejamos del meridiano, suponiendo que reducimos el radio un 0.5%. En la primera gráfica suponemos que la latitud de la mancha es de 15º (latitud promedio de las manchas analizadas) y variamos B0 entre 0º y 7º. En la segunda consideramos B0=0º, y suponemos manchas a diferentes latitudes entre 0º y 30º
Sin embargo, manteniendo fija la latitud y B0, es muy superior la dependencia respecto a una variación del radio. Así por ejemplo, si suponemos B=15º y B0=0º, y cambiamos el radio entre un 0.1% y un 0.8%, el resultado es el siguiente:
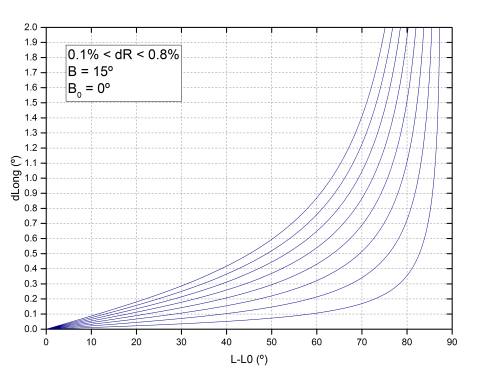
Esta gráfica es interesante porque superponiéndola a los datos se puede tener una idea aproximada de cual es la diferencia en el radio. Dada la simetría, hemos pasado todos los datos al oeste del meridiano cambiándolos de signo. Aunque la dispersión es muy alta, parece que el mejor ajuste se obtiene para valores de dR en torno al 0.4%.
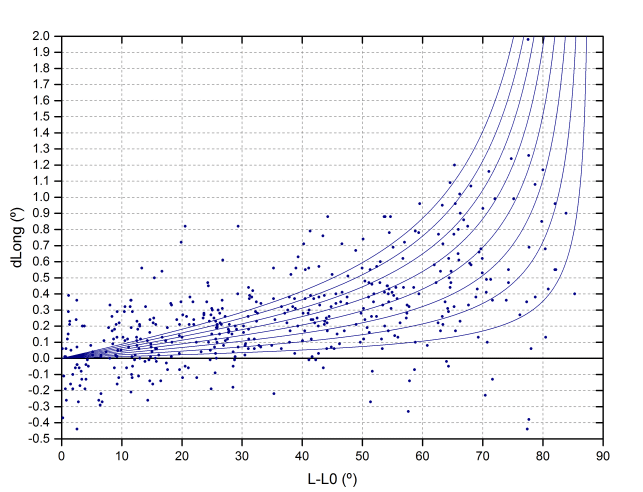
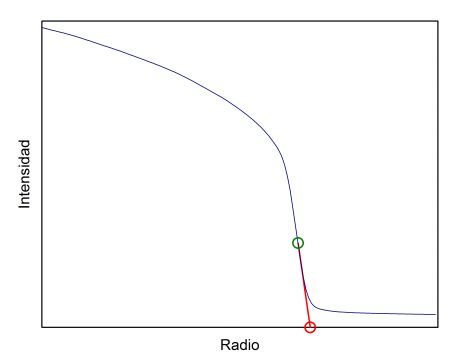
Teniendo en cuenta que no nos consta cual es el método empleado en Debrecen, en principio podemos imaginar dos causas para que exista esa diferencia en el radio. Si hacemos un corte perpendicular al limbo, la intensidad va disminuyendo desde los valores del interior del disco hasta la intensidad del fondo de cielo (ver gráfica). El programa SOL define el limbo como el punto de inflexión de dicha caída de luminosidad, es decir, el punto donde esa disminución es más rápida (círculo verde en la gráfica). Parece una elección lógica dado que, debido a la difusión atmósférica y el seeing, la luz se dispersa a ambos lados del limbo. Sin embargo, también sería posible utilizar algún otro método, como por ejemplo, el corte con el eje X de la tangente en el punto de inflexión (línea y círculo rojos). Las pruebas realizadas sobre varias imágenes sugieren que este método podría dar cuenta de la diferencia del 0.4% en el radio.
Otro efecto a tener en cuenta, aunque no actúa de forma sistemática, es la presencia de manchas muy oscuras en el interior del disco. Iris determina el radio ajustando un círculo a los píxeles que tengan la intensidad del punto de inflexión. Cuando todos esos píxeles se encuentran a lo largo del limbo, el ajuste es bueno, pero si alguna mancha es tan oscura como para llegar a esa intensidad, el programa incluye sus píxeles en el ajuste y el resultado es un círculo de radio menor. Desde la versión de 2017, SOL evita este problema, pero todas las manchas analizadas son anteriores, por lo que es un factor que no podemos descartar. Las medidas de próximos años confirmarán o no su influencia.
Javier Ruiz
Bibliografía
T. Baranyi, L. Gyóri, A. Ludmány: On-line Tools for Solar Data Compiled at the Debrecen Observatory and their Extensions with the Greenwich Sunspot Data, Solar Physics, 291, 3081-3102, 2016, DOI: 10.1007/s11207-016-0930-1
L. Gyóri, A. Ludmány, T. Baranyi: Comparative analysis of Debrecen sunspot catalogues, Monthly Notices of the Royal Astronomical Society, 465 (2), 1259-1273, 2017, DOI: 10.1093/mnras/stw2667
T. Baranyi: 2015, Comparison of Debrecen and Mount Wilson/Kodaikanal sunspot group tilt angles and the Joy's law, MNRAS, 447, (4): 1857-1865, doi:10.1093/mnras/stu2572